6 Roots Of Unity

English[edit]

For, the sum of the nth roots of unity is 0. More generally, if is a primitive nth root of unity (i.e. This is an immediate result of Vieta's formulas on the polynomial and Newton sums. If is a primitive nth root of unity, then the roots of unity can be expressed as. Pa casinos to reopen casinos. Also, don't overlook the most obvious property of all!

6 Roots Of Unity Definition

1. For, the sum of the nth roots of unity is 0. More generally, if is a primitive nth root of unity (i.e. This is an immediate result of Vieta's formulas on the polynomial and Newton sums. If is a primitive nth root of unity, then the roots of unity can be expressed as. Also, don't overlook the most obvious property of all!
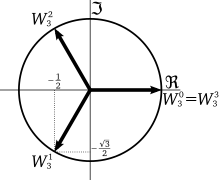
2. Roots Of Unity: When a complex number is raised to a positive integer and if it results in 1, then we say that number is a root of unity. For example: The 4th roots of unity are the numbers which.

Noun[edit]

(pluralroots of unity) New casino michigan.

6 Roots Of Unity Church

1. (number theory) An element of a given field (especially, a complex number) x such that for some positive integern, xⁿ = 1.

   In the case of the field of complex numbers, it follows from de Moivre's formula that the n{displaystyle n}n{displaystyle n}th roots of unity are cos⁡(k2πn)+isin⁡(k2πn){displaystyle textstyle cos left(k{frac {2pi }{n}}right)+isin left(k{frac {2pi }{n}}right)}, where k=1,…,n{displaystyle k=1,dots ,n}.

   • 2001, Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, page 89,

     We now show that the primitive n{displaystyle n}-th roots of unity generate the other n{displaystyle n}-th roots of unity.

   • 2003, Fernando Gouvêa, p-adic Numbers: An Introduction, Springer, page 72,

     A nice application of Hensel's Lemma is to determine which roots of unity can be found in Qp{displaystyle mathbb {Q} _{p}}.

   • 2007, Carl L. DeVito, Harmonic Analysis: A Gentle Introduction, Jones & Bartlett Learning, page 150,

     We have seen that, for a fixed value of n{displaystyle n}, the multiplicative group (Un,)˙{displaystyle (U_{n},{dot {)}}} is generated by any primitive nth root of unity. In particular, if ω{displaystyle omega } is a primitive 6th root of unity, then ω6=1{displaystyle omega ^{6}=1}, six is the smallest positive integer for which this is true, and U6={ω0,ω,ω2,ω3,ω4,ω5}{displaystyle U_{6}={omega ^{0},omega ,omega ^{2},omega ^{3},omega ^{4},omega ^{5}}}. It is easy to see that ω2{displaystyle omega ^{2}}, which is a 6th root of unity, is also a cube root of unity. The same is true of ω4{displaystyle omega ^{4}}. The element ω3{displaystyle omega ^{3}} is a square root of unity, whereas ω5{displaystyle omega ^{5}} is primitive.

Hypernyms[edit]

Holonyms[edit]

Translations[edit]

English[edit]

For, the sum of the nth roots of unity is 0. More generally, if is a primitive nth root of unity (i.e. This is an immediate result of Vieta's formulas on the polynomial and Newton sums. If is a primitive nth root of unity, then the roots of unity can be expressed as. Pa casinos to reopen casinos. Also, don't overlook the most obvious property of all!

6 Roots Of Unity Definition

1. For, the sum of the nth roots of unity is 0. More generally, if is a primitive nth root of unity (i.e. This is an immediate result of Vieta's formulas on the polynomial and Newton sums. If is a primitive nth root of unity, then the roots of unity can be expressed as. Also, don't overlook the most obvious property of all!
2. Roots Of Unity: When a complex number is raised to a positive integer and if it results in 1, then we say that number is a root of unity. For example: The 4th roots of unity are the numbers which.

Noun[edit]

(pluralroots of unity) New casino michigan.

6 Roots Of Unity Church

1. (number theory) An element of a given field (especially, a complex number) x such that for some positive integern, xⁿ = 1.

   In the case of the field of complex numbers, it follows from de Moivre's formula that the n{displaystyle n}n{displaystyle n}th roots of unity are cos⁡(k2πn)+isin⁡(k2πn){displaystyle textstyle cos left(k{frac {2pi }{n}}right)+isin left(k{frac {2pi }{n}}right)}, where k=1,…,n{displaystyle k=1,dots ,n}.

   • 2001, Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, page 89,

     We now show that the primitive n{displaystyle n}-th roots of unity generate the other n{displaystyle n}-th roots of unity.

   • 2003, Fernando Gouvêa, p-adic Numbers: An Introduction, Springer, page 72,

     A nice application of Hensel's Lemma is to determine which roots of unity can be found in Qp{displaystyle mathbb {Q} _{p}}.

   • 2007, Carl L. DeVito, Harmonic Analysis: A Gentle Introduction, Jones & Bartlett Learning, page 150,

     We have seen that, for a fixed value of n{displaystyle n}, the multiplicative group (Un,)˙{displaystyle (U_{n},{dot {)}}} is generated by any primitive nth root of unity. In particular, if ω{displaystyle omega } is a primitive 6th root of unity, then ω6=1{displaystyle omega ^{6}=1}, six is the smallest positive integer for which this is true, and U6={ω0,ω,ω2,ω3,ω4,ω5}{displaystyle U_{6}={omega ^{0},omega ,omega ^{2},omega ^{3},omega ^{4},omega ^{5}}}. It is easy to see that ω2{displaystyle omega ^{2}}, which is a 6th root of unity, is also a cube root of unity. The same is true of ω4{displaystyle omega ^{4}}. The element ω3{displaystyle omega ^{3}} is a square root of unity, whereas ω5{displaystyle omega ^{5}} is primitive.

Hypernyms[edit]

Holonyms[edit]

Translations[edit]

Further reading[edit]

6 Roots Of Unity Lutheran

• Argand system on Wikipedia.Wikipedia
• Circle group on Wikipedia.Wikipedia
• Multiplicative group#Group scheme of roots of unity on Wikipedia.Wikipedia
• Kummer ring on Wikipedia.Wikipedia